Find the Slope of the Line Graphed Below Aleks
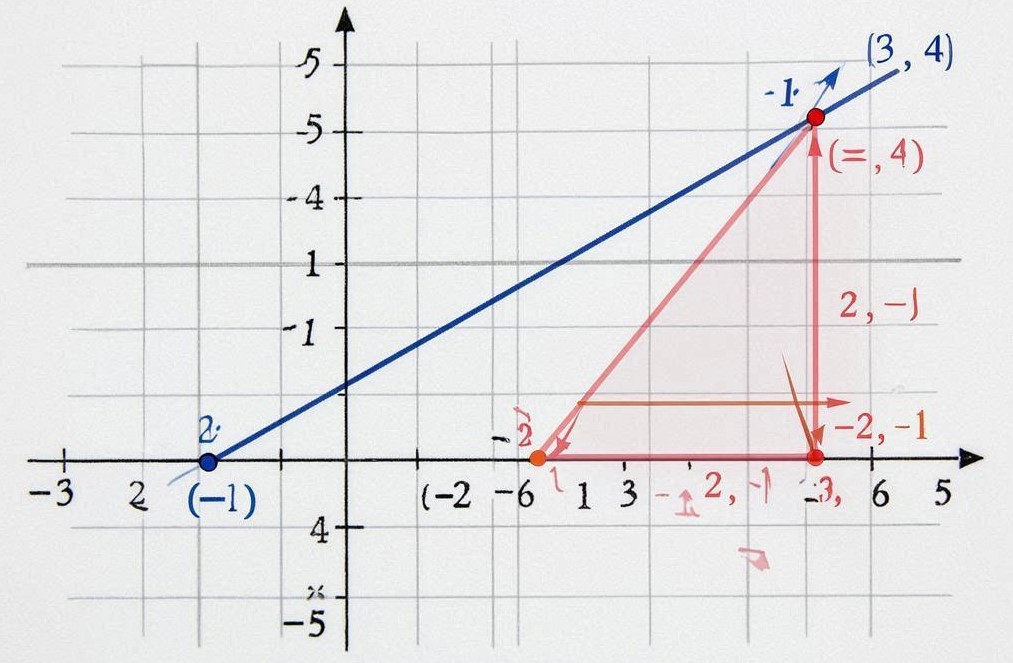
When students encounter the instruction find the slope of the line graphed below aleks, On the ALEKS learning platform, it frequently shows up in early algebra or pre-algebra classes. The purpose of this instruction is to assist students in comprehending slope as a measure of the change between two points on a line. The objective is to determine how steep the line is and how it travels across the coordinate plane, regardless of whether the graph displays a rising, descending, horizontal, or vertical line. Although ALEKS usually offers graphs that clearly show two points, students may find it difficult if they haven’t yet made the connection between slope and actual movement or visual patterns. Students use these points to practice recognizing rise over run, a skill they will return to throughout algebra. Understanding how to find the slope of the line graphed below aleks, helps build problem-solving skills essential for higher-level math.
How to Approach “Find the Slope of the Line Graphed Below ALEKS” Problems
When faced with instructions such as find the slope of the line graphed below aleks, Maintaining a consistent approach is beneficial. First, locate two distinct spots on the graph; these might be labeled coordinates or grid intersections. After selecting the spots, subtract the y-values to determine the vertical change (rising). Next, subtract the x-values to determine the horizontal change (run). Typically expressed as m = (y₂ − y₁)/(x₂ − x₁), the slope is equal to rise divided by run. This technique is effective regardless of the line’s direction. The slope will be positive if the line moves uphill from left to right, and negative if it moves downward.Knowing how to find the slope of the line graphed below aleks becomes easier with repeated practice and pattern recognition.
Why Students Struggle With “Find the Slope of the Line Graphed Below ALEKS”
Many learners find the slope of the line graphed below aleks problems challenging because they may not yet understand the visual meaning of slope. They may focus on the numbers without interpreting the graph’s direction. For instance, because the idea of “going down” over distance isn’t always intuitive, negative slopes confuse novices. Some students also misidentify the two points or accidentally reverse rise and run. When working on ALEKS, the interface might show small graphs, making it harder to read exact coordinates. Additionally, slope formulas require careful subtraction, and even small arithmetic errors can lead to incorrect results. However, when teachers educate students to evaluate slope visually—seeing how steep a line is and how it moves—these activities become more intuitive. Eventually, solving find the slope of the line graphed below aleks becomes routine.
Real-World Applications Related to ALEKS Slope Problems
Understanding slope goes far beyond solving classroom problems like find the slope of the line graphed below aleks. Slope can be found in physics, engineering, architecture, and even daily decision-making. For instance, in order to maintain accessibility and safety, ramps must adhere to specific slope criteria. Vehicle-friendly slopes are incorporated into road designs. Reading slopes is necessary even when examining graphs that monitor financial developments, weather patterns, or fitness advancements. Slope is taught early in algebra in ALEKS, preparing students for various real-world applications. Students learn to interpret the rate at which one number changes in relation to another once they understand the concept of rise over run. Finding the slope of the line graphed below Alek’s type of activity is crucial for broader analytical skills because it gives pupils the clarity they need to examine graphs confidently.
Tips for Mastering “Find the Slope of the Line Graphed Below ALEKS” Questions
To improve accuracy when solving find the slope of the line graphed below aleks tasks, students should practice consistent strategies. Start by locating the points on the graph that are easiest to see, ideally those that are right on grid intersections. To lessen the possibility of confusing rise and run, always write down the slope formula before entering the values. Sketching the rise and run graphically is another useful tip: count the number of units the line moves upward or downward, followed by the number of units it moves horizontally. Students should keep in mind that downward movement results in negative increase when dealing with negative slopes. It is also helpful to check the final answer rationally, since the answer cannot be negative if the line slopes upward. With practice, learners become confident and accurate in solving find the slope of the line graphed below aleks, no matter the complexity of the graph.
Conclusion
Mastering problems like find the slope of the line graphed below aleks provides a strong foundation for success in algebra and beyond. A fundamental idea in mathematics, slope can be found in many advanced subjects, such as calculus, graph interpretation, linear equations, and real-world modeling. Students gain analytical thinking and visual reasoning skills by learning how to recognize two points, compute rise over run, and determine a line’s direction. Through organized practice and understandable graphics that boost confidence, ALEKS strengthens these skills. As students continue to experience slope in both academic and practical settings, the strategies developed from solving find the slope of the line graphed below aleks will remain valuable tools that support long-term mathematical growth and understanding.